MATHEMATICAL FORMULAS
OF THE POTENTIAL PAYBACK PERIOD (PPP)
AND THE INTERNAL RATE OF RETURN (IRR)

I – POTENTIAL PAYBACK PERIOD

The Potential Payback Period (PPP) for stock valuation is defined as the period of time necessary to equalize the current share price with the sum of future earnings per share. It is a mathematical adjustment of the traditional P/E ratio (PER) to earnings growth rate, thus allowing more meaningful stock comparisons.

Future earnings are discounted to their present values using a long-term interest rate as the discount rate, thus mathematically involving interest rates in stock valuation.

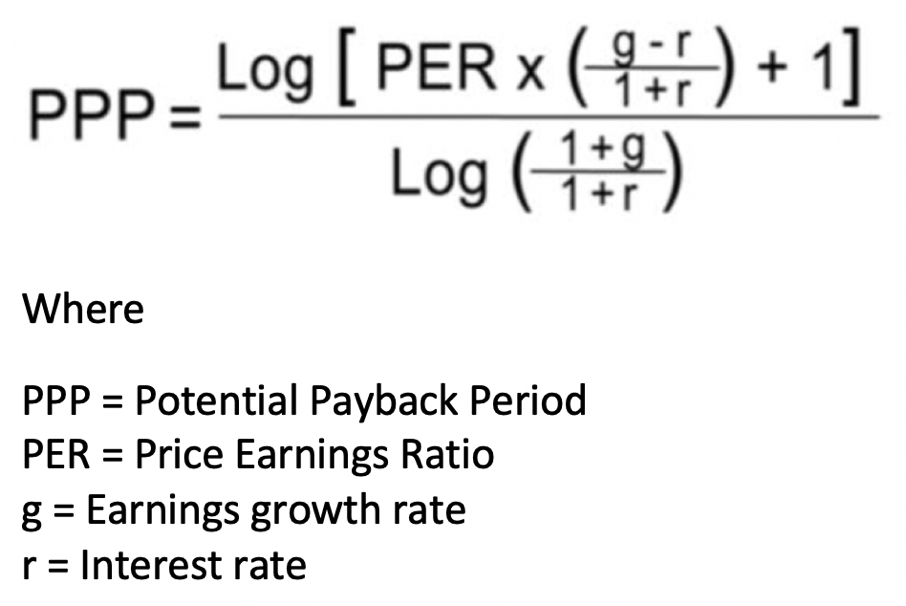
For more details go to https://stockinternalrateofreturn.com/index.html

The formula of the Potential Payback Period (PPP) for stock valuation is based on that of the sum of the first n terms of a geometric sequence.

Sum of the first n terms of a geometric sequence

Consider the geometric progression: E₀ , E₀q , E₀q², E₀q³, ………… E₀q^n-1,
Let’s the sum of n terms be P, the first term be E0 and the common ratio of geometric progression be q.

Then P = E₀ + E₀q + E₀q² + E₀q³ + ……. + E₀q^n-1 (1)

Multiply both sides of P by q, we get,

Pq = E₀q + E₀q² + E₀q³ + ……. + E₀qⁿ (2)

Subtracting (2) from (1), we get,

Pq - P = (E₀q + E₀q² + E₀q³ + … + E₀qⁿ) – (E₀ + E₀q + E₀q² + E₀q³ + ……. + E₀q^n-1)
Pq - P = E₀qⁿ – E₀
P (q – 1) = E₀ (qⁿ – 1)
P = E₀ (qⁿ – 1) / (q – 1)

Hence the sum of n terms of the geometric sequence is P = E₀ (qⁿ – 1) / (q – 1)

P/E₀ = (qⁿ – 1) / (q – 1)

Now let’s calculate n, which is the Potential Payback Period (PPP), while

P is the current share price.
E₀ is the earnings per share for the current year.
P/E₀ is the Price Earnings Ratio (PER) , which we name X for now.

X = (qⁿ – 1) / (q – 1)
qⁿ – 1 = X (q – 1)
qⁿ = X (q – 1) + 1
Log qⁿ = Log [X (q – 1) + 1]
n Log q = Log [X (q – 1) + 1]
n = Log [X (q – 1) + 1] / Log q

In our sequence of future earnings per share, the common ratio q of geometric progression is, based on the compound interest formula and the discount rate formula, as follows:
q = (1+g) / (1+r)
where
g = earnings per share growth rate
r = long-term interest rate used as discount rate to discount future earnings per share to their present values.

In the above equation with n on the left side,
(q – 1) = [(1 + g) / (1 + r)] - [(1 + r) / (1 + r)] = (g - r) / (1 + r)
and
X is the Price Earnings Ratio (PER)

Then finally,
n = Log [PER X [(g - r) /(1+r)] + 1] / Log [(1 + g) / (1 + r)]
n is the Potential Payback Period (PPP).
PPP = Log [PER X [(g - r)/(1+r)] + 1] / Log [(1 + g) / (1 + r)]

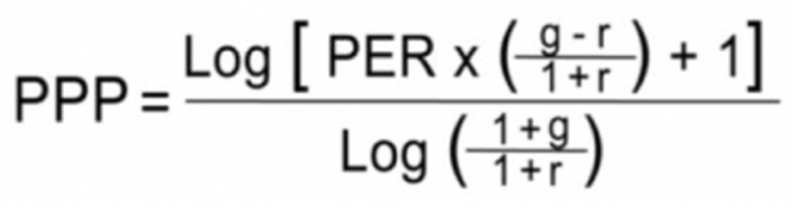
II – INTERNAL RATE OF RETURN

A stock’s internal rate of return (IRR) is the return rate that allows the sum of future earnings per share to equalize the current share price P over a number of years corresponding to the stock’s potential payback period (PPP). The share’s holder will then see the share’s value increase twofold, from P to 2P.

The IRR formula is therefore directly derived from the PPP formula.

P X (1 + IRR)^PPP = 2 P
(1 + IRR)^PPP = 2
1 + IRR = 2^1/PPP
IRR = 2^1/PPP - 1

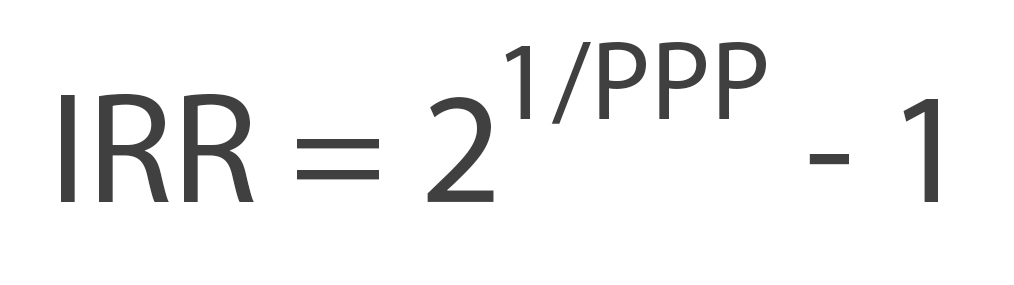
From the PPP formula as shown above, the IRR formula can also be written like this,

(END)