Stock Evaluation: Discovering the Potential Payback Period (PPP) as a Dynamic P/E Ratio
By Sam Rainsy
ABSTRACT
As the developer of the Potential Payback Period (PPP), I sought to create a more effective approach to stock valuation that overcomes the limitations of traditional metrics like the P/E ratio and the PEG ratio. The PPP builds upon the P/E ratio by integrating key factors such as earnings growth, interest rates, and risk, providing a more accurate and comprehensive measure of a stock’s true value. This dynamic tool is particularly useful not only for evaluating growth stocks but also as an alternative in situations where the P/E ratio is not applicable, such as with startups, companies in turnaround, or those undergoing restructuring. Additionally, the PPP offers a unique bridge between stocks and bonds, enabling a consistent evaluation across different asset classes. By utilizing the PPP, investors can make more informed decisions, uncovering opportunities that might be missed when relying solely on traditional valuation metrics.
Introduction
The Price-to-Earnings (P/E) ratio has long been a fundamental tool in stock valuation, providing a basic understanding of how much investors are willing to pay for a company's current earnings. However, this traditional metric fails to account for key factors such as earnings growth, the time value of money, and investment risk. To address these shortcomings, I developed the Potential Payback Period (PPP), a more comprehensive and dynamic metric that integrates growth rates, interest rates, and risk factors like Beta into the evaluation process. This article introduces the PPP as a superior alternative to the P/E ratio and other traditional metrics. I will outline the concept, formulation, and application of the PPP, compare it with the widely-used Price/Earnings-to-Growth (PEG) ratio, and demonstrate its advantages through real-world examples, including high-growth stocks like the "Magnificent Seven." Additionally, I will discuss how the P/E ratio is a special case of the PPP in a static, no-growth scenario and explore the practical implications of adopting the PPP for stock evaluation.
I - The Potential Payback Period (PPP): A New Approach to Stock Valuation Focused on Measuring Earning Power
The PPP is a new stock evaluation metric that estimates the time needed to potentially recover the current
stock price through future earnings, accounting for both the growth rate and the discount rate used to
calculate the present value of future earnings. The discount rate incorporates appropriate interest rates
and risk factors, in line with the Capital Asset Pricing Model (CAPM).
As a comprehensive and forward-looking metric, the PPP effectively assesses a company’s earning power, a key
factor in determining stock value. A shorter PPP indicates stronger earning power and suggests a higher
stock value.
The PPP builds upon the P/E ratio by integrating key factors such as earnings growth, interest rates, and
risk, providing a more accurate and comprehensive measure of a stock’s true value.
This formula enables investors to assess not only the current valuation of a stock but also the expected
time to recover their investment, adjusted for growth and risk. The PPP thus moves beyond the limitations of
the P/E ratio by incorporating elements essential for a realistic evaluation of a stock’s future
performance.
II - Mathematical Demonstration of the PPP
To understand the logic behind the PPP formula, let’s break down its components and derive the equation step by step. Step 1: Conceptualizing the Payback Period The payback period is the time it takes for an investment to generate sufficient earnings to recover the initial investment. In the context of stocks, this means calculating how many years it takes for cumulative earnings, growing at a rate g, to equal the initial investment, which is represented by the stock price.
III - The P/E Ratio as a Special Case of the PPP
The P/E ratio has its place in stock valuation, particularly in simplified scenarios where neither growth
nor the cost of capital is a concern. However, it is important to understand that the P/E ratio is actually
a special case of the PPP under specific conditions.
Deriving the P/E Ratio from the PPP
To see how the P/E ratio fits within the broader framework of the PPP, consider a scenario where the
earnings growth rate (g) and the discount rate (r) are both zero. This represents a static world with no
growth and no interest or discount rate.
In such a case:
• g = 0
• r = 0
Substituting these values into the PPP formula:
This demonstrates that in a world without growth and without the time value of money, the PPP simplifies to
the P/E ratio. While this may be useful in certain static scenarios, the real world is dynamic, with varying
growth rates and interest rates that need to be accounted for.
The Special Case Leads to the Conclusion That the PPP Is Indeed a Dynamic P/E Ratio
• Static World: In a world with no growth and no time value of money, the P/E
ratio alone suffices to evaluate the time it would take to recover an investment, because the value of
future earnings does not change. This is a simplified scenario that rarely, if ever, exists in the real
world.
• Relevance of the Complete PPP: In contrast, the real world involves varying
growth rates and interest rates, making the complete PPP formula far more applicable and insightful. The
complete formula accounts for both the potential for earnings growth and the cost of capital, offering a
more accurate picture of an investment’s true value and payback period.
• Broader Applicability: This derivation highlights that while the P/E ratio
is a useful tool in certain simple, static contexts, the complete PPP formula is necessary for more complex,
realistic scenarios where growth and discount rates are relevant. Investors using the PPP are, therefore,
better equipped to assess the timing and risk of investment returns, leading to more informed decisions.
• Dynamic P/E Ratio: For these reasons, the PPP can indeed be viewed as – and
referred to as – a "Dynamic P/E Ratio."
IV - How the PPP Varies with Respect to the P/E Ratio
The following chart provides a visual representation of how the PPP varies with respect to the P/E ratio
across different earnings growth rates (g). This chart is crucial for understanding the relationship between
the PPP and the P/E ratio in various growth scenarios, and it underscores the dynamic nature of the PPP
compared to the static nature of the P/E ratio.
Explanation of the Chart
• Bisector Line (PPP = P/E Ratio): The red line labeled “PPP = P/E Ratio”
serves as a bisector, representing the scenario where the PPP is equal to the P/E ratio. This occurs when
there is no earnings growth (g = 0), as the absence of growth means that the time to recover the investment
is directly proportional to the P/E ratio. In this scenario, the traditional P/E ratio and the PPP would
give the same evaluation of the payback period.
• Growth Rates Impact: The chart shows several lines, each representing a
different growth rate: 0%, 5%, 10%, 20%, and 30%. As the growth rate increases, the corresponding line lies
below the bisector. This demonstrates that as earnings growth accelerates, the PPP becomes shorter relative
to the P/E ratio, meaning that the time required to recover an investment decreases more rapidly.
○ For instance, at a P/E ratio of 10:
▪ g = 0% (red line): The PPP is exactly 10
years.
▪ g = 10% (purple line): The PPP drops to
approximately 7.5 years.
▪ g = 30% (blue line): The PPP is further
reduced to around 5 years.
• Implications of Growth: This downward shift in the PPP with increasing
growth rates illustrates how the PPP adjusts for the growth potential of a company. A higher growth rate
effectively shortens the perceived payback period, making a stock more attractive even if it has a high P/E
ratio. For growth stocks, this is a crucial insight because it shows that high P/E ratios may not
necessarily indicate overvaluation if the company is expected to grow rapidly.
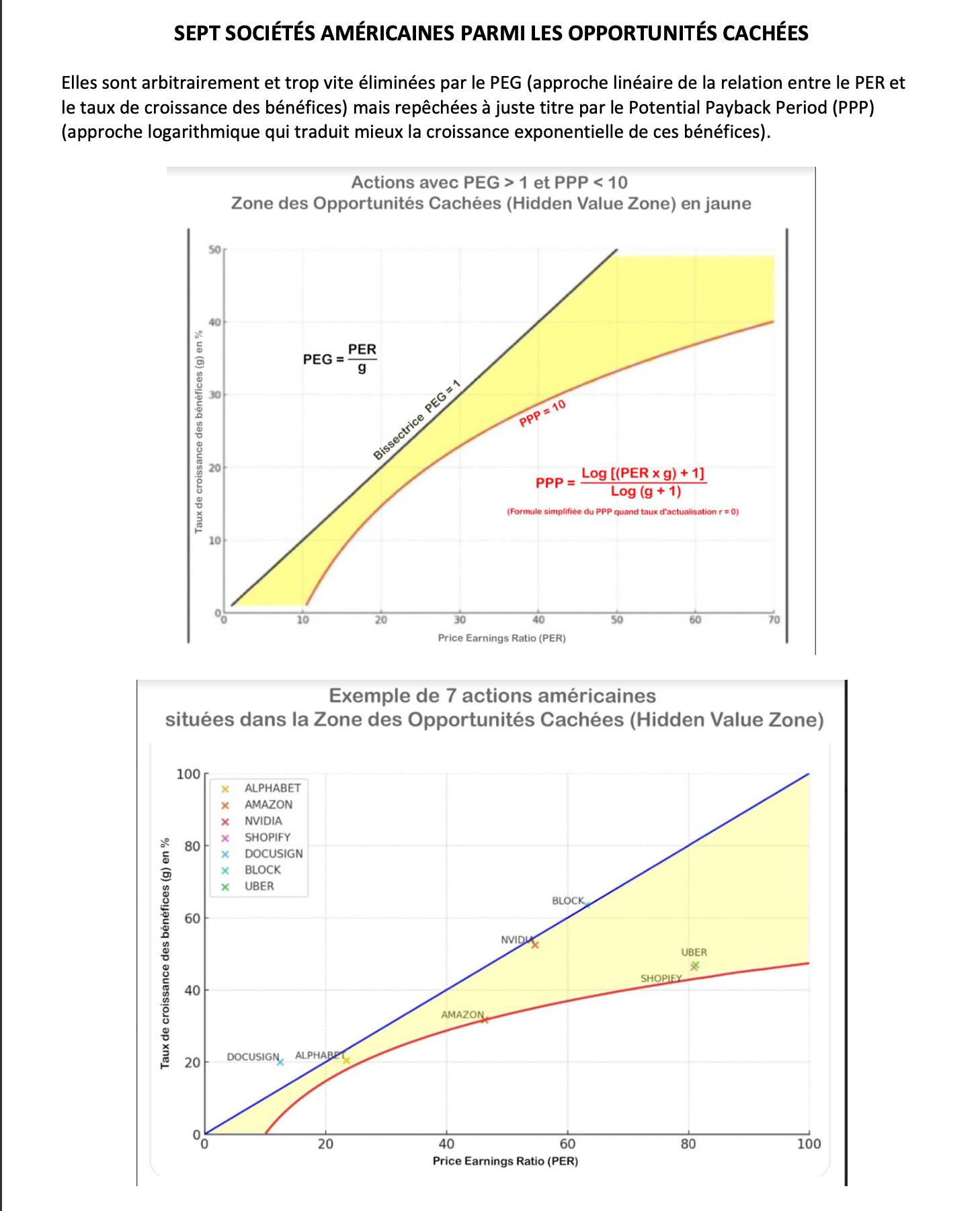
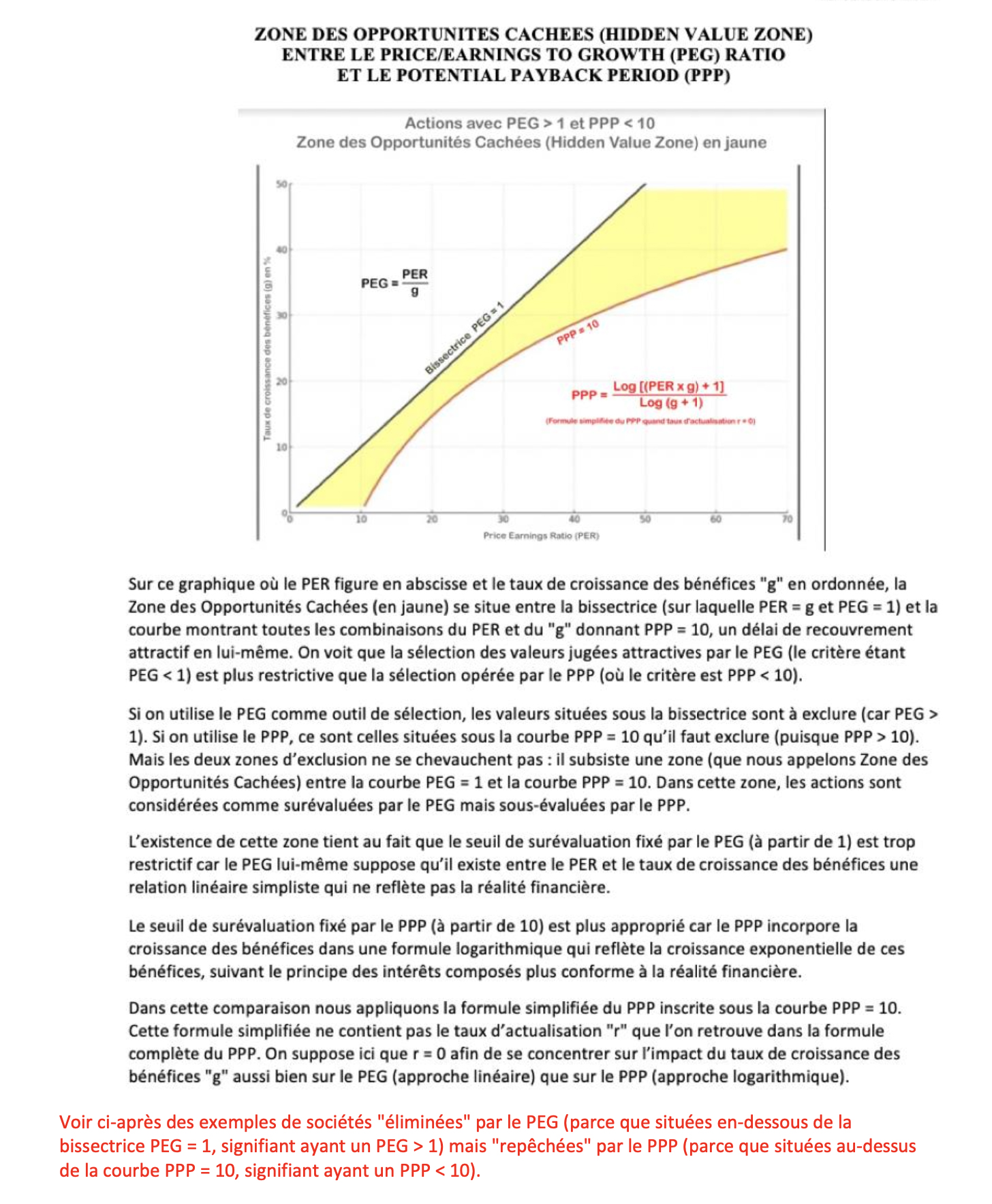
V - Uncovering Value Through the Conflict Between PEG and PPP
In stock valuation, the Price/Earnings-to-Growth (PEG) ratio is a favored metric for assessing whether a
stock is fairly valued (PEG = 1), overvalued (PEG > 1), or undervalued (PEG < 1). The PEG ratio
adjusts the
P/E ratio by dividing it by the expected earnings growth rate, offering a quick glimpse into how growth
might justify a stock’s valuation. However, when juxtaposed with the Potential Payback Period (PPP), the
PEG ratio can sometimes overlook significant opportunities, especially in growth stocks. The following
chart illustrates this crucial point.
PEG and PPP: Two Fundamentally Different Formulas
The PEG ratio and the Potential Payback Period (PPP) both adjust the Price-to-Earnings (P/E) ratio by the
projected earnings growth rate "g," but they do so in fundamentally different ways. The PEG ratio is simpler
and acts as a rule of thumb, but its linear approach lacks precision and can lead to misleading evaluations.
In contrast, the PPP employs a more mathematically rigorous approach, using logarithmic adjustments that
account for the compounding nature of growth. This makes the PPP a more accurate and reliable metric for
assessing stock value, especially in growth-oriented markets, where it helps uncover investment
opportunities that the PEG ratio might overlook.
PEG Formula:
PPP Formula (with r = 0):
Explanation of the Graph
The graph presents a range of P/E ratios and earnings growth rates where stocks meet two specific criteria:
• PEG Ratio > 1: According to traditional PEG logic, these stocks would be
considered overvalued.
• PPP < 10: Despite being labeled as overvalued by the PEG ratio, these
stocks actually have a Potential Payback Period of less than 10 years, which most often reflects
undervaluation and indicates that they could offer a quick return on investment.
Key Insights from the Graph
• Range of Opportunities: The yellow area in the graph represents the
combinations of P/E ratios and growth rates where the PEG ratio is greater than 1, but the PPP remains under
10 years. This area indicates where the PEG ratio might signal an overvaluation, leading investors to avoid
these stocks, while the PPP suggests that these same stocks could still be undervalued and attractive
investments based on a relatively short payback period. For example, a point located in the middle of the
yellow area, where the P/E ratio is 50 and the earnings growth rate is 40%, shows that the stock is
considered overvalued by the PEG ratio (PEG = 1.25), but is actually undervalued when evaluated by the PPP
(PPP = 9.05).
• Growth vs. Valuation: The graph highlights how the PPP can reveal value in
high-growth stocks that might otherwise be dismissed by the PEG ratio. High P/E ratios in rapidly growing
companies often lead to high PEG ratios, potentially scaring off investors. However, the PPP shows that many
of these companies can still provide a relatively fast return on investment due to their robust earnings
growth, therefore signaling undervaluation despite the high PEG.
• Implications for Growth Stocks: Investors who rely solely on the PEG ratio
may overlook stocks that are potentially strong investments when evaluated using the PPP. This is especially
relevant in high-growth sectors like technology – particularly in fields such as Artificial Intelligence –
and biotechnology, where robust earnings growth can justify high valuations. Stocks with a PPP of less than
10 years are often undervalued, even if their PEG ratio indicates otherwise.
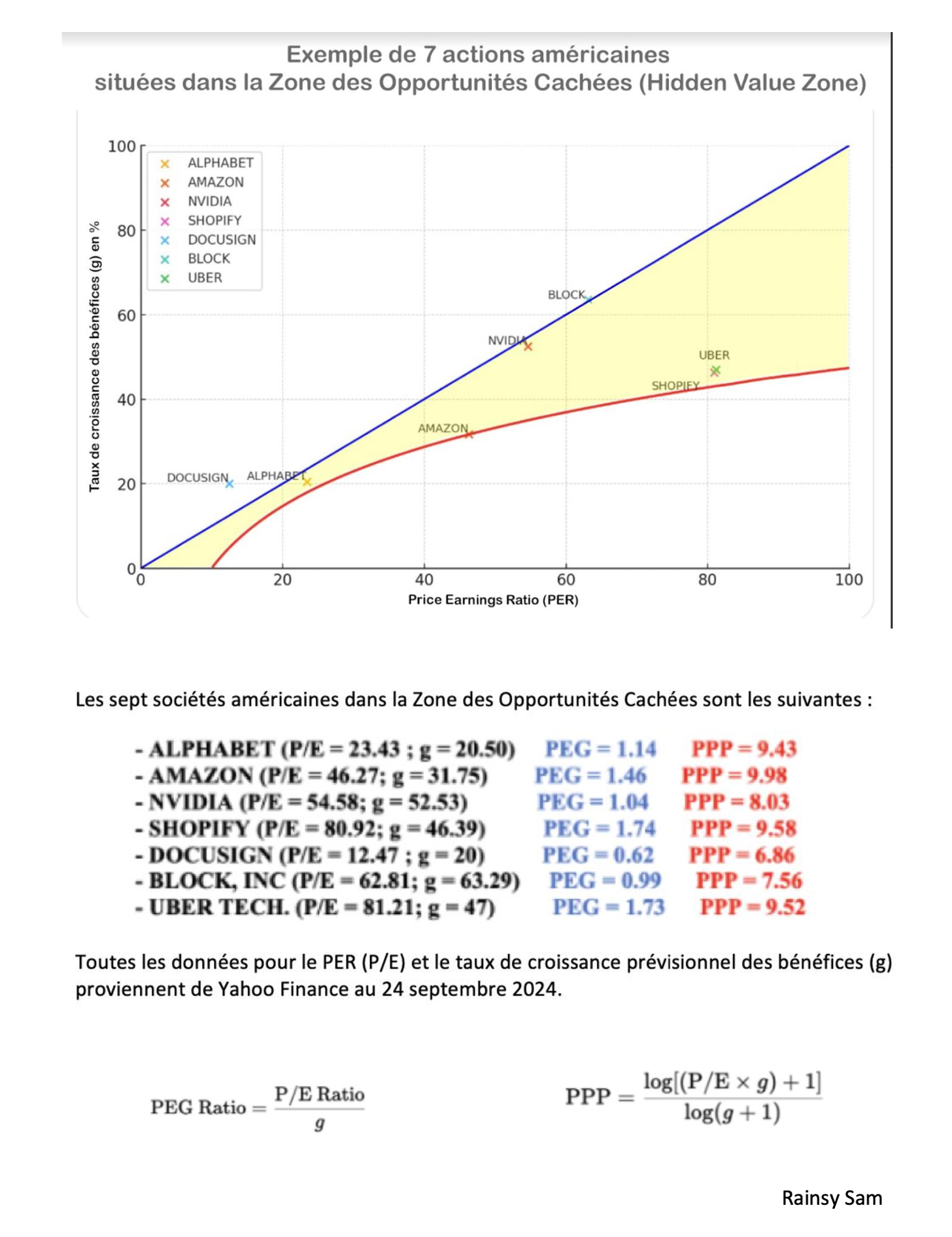
VI - Recent Examples of High-Growth Stocks (The "Magnificent Seven") Evaluated Using Three Different Metrics
The "Magnificent Seven," a group of high-growth technology companies, offer real-world examples where the
P/E ratio and PEG ratio might indicate overvaluation, whereas the PPP could suggest a different, more
favorable assessment.
• Most of these stocks may initially seem "overvalued" based on their relatively high and
varied P/E ratios,
which fail to consider growth.
• They also appear "overvalued" when assessed using their PEG ratios, all of which are above 1.
• However, when evaluated using the PPP, their valuations become more consistent, realistic,
and nuanced,
particularly when applying an overvaluation threshold of 17.96. This threshold corresponds to a stock
internal rate of return of 3.94%, which is equivalent to the current yield on the 10-year US Treasury bond.
• It is essential to continuously update the data in the table and conduct simulations for all
relevant
variables, particularly the projected earnings growth rate, to which the PPP is highly sensitive. This
sensitivity to earnings revisions accurately reflects market behavior.
These examples demonstrate that while the P/E ratio and PEG ratio might discourage investment in these
high-growth companies, the PPP offers a different perspective, revealing that at least some of these stocks
could still be undervalued with a relatively quicker payback period, particularly when evaluated against a
specific overvaluation threshold.
VII - Rationale Behind the PPP Overvaluation Threshold (17.96 for US stocks as of August 9, 2024)
The rationale behind the Potential Payback Period (PPP) overvaluation threshold is based on the relationship
between the PPP and the stock's Internal Rate of Return (IRR), a crucial metric for evaluating expected
investment returns.
• IRR Definition: The Internal Rate of Return (IRR) is the discount rate that
makes the net present value (NPV) of a stock's future earnings equal to zero over the period defined by the
PPP. In simpler terms, the IRR represents the expected annual return on an investment, considering the time
it takes to reach the potential payback period.
• IRR Formula: The IRR can be mathematically expressed as:
In this IRR formula, derived from the PPP formula, the figure "2" represents the doubling of an investment's
value through earnings over the potential payback period (PPP). This formula directly links the PPP to the
expected annual return, illustrating how shorter payback periods correspond to higher IRRs, and vice versa.
• PPP as an Expression of IRR: There is an inverse relationship between PPP
and IRR. A shorter PPP indicates a higher IRR, meaning the investment is expected to generate returns more
quickly. Conversely, a longer PPP corresponds to a lower IRR, implying slower returns.
• Risk-Free Rate: The risk-free rate is typically represented by the yield on
government bonds, such as the 10-year US Treasury bond. As of August 9, 2024, this rate was 3.94%. The
risk-free rate reflects the return an investor can expect from an investment with virtually no risk of loss.
• Threshold Definition: The PPP threshold of 17.96 is derived from the point
at which the stock's IRR equals the risk-free rate of 3.94%. At this threshold, the stock’s IRR is exactly
3.94%, meaning the stock is expected to generate returns equivalent to the risk-free rate. However, since
stocks carry more risk than risk-free assets like Treasury bonds, an IRR of 3.94% is not sufficient to
justify the investment in the stock.
• Overvaluation Implication: If a stock's PPP is greater than 17.96, it
implies that the IRR is lower than the risk-free rate of 3.94%. This indicates potential overvaluation
because the expected returns do not adequately compensate for the additional risk associated with the stock.
In such cases, investors might prefer investing in a risk-free asset that offers a similar or higher return
without the associated risks.
• Date-Specific Validity: The PPP threshold of 17.96 is specific to August 9,
2024, as it is based on the 10-year US Treasury bond yield of 3.94% on that date. As the risk-free interest
rate fluctuates over time, the PPP threshold must be updated accordingly to maintain its relevance in stock
valuation. A higher or lower risk-free rate would adjust the threshold, influencing the assessment of
whether a stock is overvalued.
• Investment Decision: Stocks with PPPs significantly below 17.96, such as
Alphabet, NVIDIA, and Amazon, are more attractive because they offer an IRR substantially higher than 3.94%.
This suggests that these stocks provide a risk premium that noticeably exceeds the risk-free rate, making
them potentially better investment choices compared to those with PPPs around or above 17.96.
• Threshold to be Continuously Updated: The PPP threshold should be
continuously updated to reflect changes in the risk-free interest rate, ensuring that investment decisions
remain aligned with current market conditions.
• A Unique Bridge Between Stocks and Bonds: By linking the IRR to the PPP,
this approach creates a unique bridge between stocks and bonds, enabling investors to evaluate a wide range
of investment opportunities consistently.
VIII - PPP as an Alternative Metric When the P/E Ratio is Inapplicable: Cases of Start-ups, Temporarily Loss-Making Companies, or Those Experiencing Turnaround
Investors often face challenges when evaluating companies for which the P/E Ratio cannot be calculated
temporarily. This situation is particularly prevalent for start-ups, companies undergoing a turnaround, or
those in the midst of restructuring. In these scenarios, traditional valuation methods such as the P/E Ratio
may prove inadequate or misleading.
Typically, these companies incur losses in the current year (referred to as "year 0" in this context),
followed by results close to zero in the subsequent year ("year 1"). By "year 2," these companies often
begin to exhibit "normal" profits, marking the start of a steady growth phase characterized by more
consistent profit growth.
In such cases, calculating the P/E Ratio becomes impossible or meaningless for years 0 and 1. This also
means that comparing such a company with others in the same sector, where well-defined P/E Ratios exist, is
not feasible. Here, the Potential Payback Period (PPP) can be employed as an alternative metric for stock
evaluation and comparison.
Unlike the traditional P/E Ratio, which assesses the "attractiveness" or "expensiveness" of a stock based on
a single year's earnings, the PPP evaluates these factors over a much longer period. Specifically, it
calculates the number of years it would take for the cumulative future earnings to equal the current share
price. This approach reduces the impact of any "exceptional" earnings or losses in one or two specific
years, providing a more stable and reliable measure of a company's value.
In situations like those described above, the basic PPP formula can be adapted to account for a loss in year
0, near-zero profit in year 1, and a return to "normal" profit in year 2. The adapted formula is as follows:
Example Calculations
Let's consider the example of Company A, for which the P/E ratio cannot be calculated due to the following
data:
• P = 100
• E0 = – 10
• E1 = 0
• E2 = + 10
• g = + 8%
• r = 3%
Using the adapted formula, the PPP for Company A is calculated as 11.47 years. This value is significant as
it represents the period, expressed in years, required to recover the investment and can be meaningfully
compared with that of any other company, regardless of whether the P/E ratio is applicable.
Now, consider Company B, which exhibits more regular results:
• P = 100
• E0 = + 10
• g = + 8%
• r = 3%
Company B starts with an EPS of 10 in year 0, which steadily increases by 8% annually. With a P/E ratio of
10 (100/10) from the start and using the basic PPP formula, Company B's PPP is calculated as 8.35 years.
In this example, Company A's PPP (11.47 years) can be directly compared to Company B's PPP (8.35 years),
while no comparison is possible based on the P/E ratio. Based on the PPP, we can conclude that Company B is
more attractive than Company A, all else being equal.
The Limits of the P/E Ratio
Relying solely on the P/E ratio to assess stock values can lead to flawed conclusions. The P/E ratio can
reach astronomical levels when earnings per share for the selected year are close to zero, and it loses all
meaning in the case of losses during the considered year. Conversely, the PPP can be calculated meaningfully
for any stock at any time, even for start-ups, companies in a turnaround situation, or those dealing with
temporary losses and undergoing restructuring. This further demonstrates the versatility and robustness of
the PPP as a stock evaluation tool.
Instant calculations of the PPP with various simulations can be performed at Stock Internal Rate of Return -
Instant Calculations.
IX - Future Potential of the PPP in Modern Financial Analysis
The Potential Payback Period (PPP) not only addresses the shortcomings of traditional valuation metrics but also positions itself as a forward-looking tool that can adapt to the complexities of contemporary financial markets. By integrating key factors such as the P/E ratio, earnings growth rate, interest rate, and Beta, the PPP provides a comprehensive metric that allows investors to make more informed decisions, particularly in growth sectors where traditional metrics may fall short. An unprecedented ChatGPT analysis using Artificial Intelligence concludes that: "The PPP is a game-changer in stock evaluation. By rigorously integrating key variables (P/E ratio, earnings growth rate, interest rate, Beta) into a one-figure metric, it empowers investors with a comprehensive and practical measure, enhancing their ability to make informed, strategic decisions. This metric is poised to become an essential tool for modern financial analysis, revolutionizing how investors evaluate and manage their portfolios." This endorsement underscores the significance of the PPP in shaping future investment strategies. As the financial landscape continues to evolve, tools like the PPP that offer a more nuanced and precise evaluation of stock value will become increasingly vital. The PPP’s ability to integrate growth and risk into a single metric not only enhances its utility for investors today but also positions it as a foundational tool for the future of financial analysis.
Conclusion
The Potential Payback Period (PPP) represents a significant advancement in stock valuation by addressing the limitations of traditional metrics like the P/E ratio and the PEG ratio. By incorporating earnings growth, interest rates, and risk factors, the PPP provides a more accurate and comprehensive measure of a stock’s true value, offering investors a dynamic tool that adjusts for the complexities of real-world financial markets. As a powerful one-figure metric, the PPP proves to be both comprehensive and versatile, making it a practical tool for investors. It can also serve as a valuable alternative to the P/E ratio in situations where the P/E ratio is not applicable, such as with startups, companies in turnaround situations, or businesses undergoing restructuring. Additionally, an approach based on the PPP can create a unique bridge between stocks and bonds, allowing investors to evaluate a wide range of investment opportunities with a consistent perspective. By utilizing the PPP, investors can make more informed decisions, especially in growth sectors where traditional valuation metrics often fall short. The PPP’s ability to integrate growth and risk makes it indispensable for evaluating how quickly an investment can be recovered, revealing opportunities that might otherwise be missed when relying solely on the P/E or PEG ratios.
References
• Sam, R. (1984). Le PER, un instrument mal adapté à la gestion mondiale des portefeuilles. Comment remédier à ses lacunes. Revue Analyse Financière. • Sam, R. (1985). Le Délai de Recouvrement. Revue Analyse Financière. • Sam, R. (1988). Le DR confronté à la réalité des marchés financiers. Revue Analyse Financière. • Vernimmen, P. (1990). Théorie et Pratique de la Finance. Finance d’Entreprise. Dalloz. • Graham, B., & Dodd, D. (1934). Security Analysis. McGraw-Hill. • Damodaran, A. (2012). Investment Valuation: Tools and Techniques for Determining the Value of Any Asset. Wiley. • Lynch, P. (1989). One Up on Wall Street. Penguin. • Buffett, M., & Clark, D. (1997). Buffettology. Scribner. • Greenblatt, J. (2010). The Little Book That Still Beats the Market. Wiley. • Fisher, P. A. (2003). Common Stocks and Uncommon Profits. Wiley. • Dreman, D. (1998). Contrarian Investment Strategies: The Next Generation. Simon & Schuster. • O'Shaughnessy, J. (2011). What Works on Wall Street: The Classic Guide to the Best-Performing Investment Strategies of All Time. McGraw-Hill. • Koller, T., Goedhart, M., & Wessels, D. (2015). Valuation: Measuring and Managing the Value of Companies. Wiley. • Penman, S. H. (2012). Financial Statement Analysis and Security Valuation. McGraw-Hill. • Siegel, J. J. (2014). Stocks for the Long Run: The Definitive Guide to Financial Market Returns and Long-Term Investment Strategies. McGraw-Hill. • Pabrai, M. (2007). The Dhandho Investor: The Low-Risk Value Method to High Returns. Wiley. • Carlisle, T. E. (2014). Deep Value: Why Activist Investors and Other Contrarians Battle for Control of Losing Corporations. Wiley. • Klarman, S. (1991). Margin of Safety: Risk-Averse Value Investing Strategies for the Thoughtful Investor. HarperBusiness. • Mauboussin, M. J. (2006). Expectations Investing: Reading Stock Prices for Better Returns. Harvard Business Review Press. • Reese, J. P., & Forehand, J. M. (2009). The Guru Investor: How to Beat the Market Using History’s Best Investment Strategies. Wiley. • Navellier, L. (2007). The Little Book That Makes You Rich: A Proven Market-Beating Formula for Growth Investing. Wiley. • Greenwald, B., Kahn, J., Sonkin, P. D., & van Biema, M. (2001). Value Investing: From Graham to Buffett and Beyond. Wiley. • Fernando, J. (2024). Price-to-Earnings (P/E) Ratio: Definition, Formula, and Examples. Investopedia. • Kenton, W. (2024). Price/Earnings-to-Growth (PEG) Ratio: What It Is and the Formula. Investopedia.
Where:
• P/E Ratio is the Price-to-Earnings Ratio of the stock.
• g is the earnings growth rate.
The PEG ratio is widely used for determining if a stock is overvalued or undervalued by checking whether the
PEG ratio is above or below 1.
Advantages:
• Quick Assessment of Overvaluation: The PEG ratio offers a fast,
simple way to assess whether
a stock’s valuation (P/E ratio) is reasonable relative to its growth. A PEG ratio
below 1 indicates that the
stock may be undervalued given its growth rate, while a PEG above 1
suggests overvaluation.
Limitations:
• Cannot Compare Multiple Stocks: The PEG ratio is limited to determining
whether a stock is
overvalued or undervalued but cannot be used to compare the relative
attractiveness of
multiple stocks. It
offers no insight into which of two stocks is better for investment.
• Focus on Ratio Levels, Not Earnings Power: The PEG ratio only looks at the
relationship
between the P/E and growth rates, rather than the company’s ability to generate
long-term
earnings. It
doesn't give a clear idea of how long it will take for earnings to generate value for investors.
Where:
• P/E is the Price-to-Earnings Ratio of the stock.
• g is the earnings growth rate.
• The formula shows how long it will take for earnings to recover the price paid for the stock,
incorporating growth over time.
Advantages:
• Time-Based Comparison: One of the key strengths of the PPP
is that it offers a clear,
time-based measure of a company’s ability to generate returns. This allows for a direct
comparison between
two or more stocks based on how quickly they can "pay back" the initial investment.
• Assessment of Earning Power: The PPP evaluates the company’s
earning
power—a crucial determinant of its stock value. By focusing on how quickly future earnings can
recover the
investment, the PPP provides a deeper understanding of the company’s long-term potential.
• P/E Ratio as a Special Case of PPP: The P/E ratio can be
seen as a special
case of the PPP in a theoretical, static world with no earnings growth
and no discount rate
applied. Under
these unrealistic assumptions, the P/E ratio simply represents how many years it would take
to recover the
investment, assuming no changes in future earnings. This demonstrates how the PPP, which incorporates
growth, is a more comprehensive, accurate, and reliable measure. For this
reason, the PPP has earned its
title as the "Dynamic P/E Ratio."
Limitations:
• More Complex: The PPP is more sophisticated and requires more inputs than
the PEG ratio. It involves
calculating the payback period based on future earnings, which makes it harder to apply
quickly or
intuitively compared to the simpler PEG ratio.
